Is high res audio BS? - Sampling rate

 So I heave heard a lot of argument both ways, sometimes coming from very knowledgable people.  

There are two parts to this, the sampling frequency (i.e. 44.1 vs 48khz vs 90kphz), and the bit depth (i.e. 8 bit 16 bit vs 24 bit)

To summarize the arguments.

• On the one hand, higher bitrates means more accurate sampling, right?  44.1 Khz is very clearly better than the 8Khz originally used for land line phones, so more is always better!
• On the other hand, the NyQuest theorum says that a sample 2x the highest frequency you want to sample is fine, so for 20khz tones, a 40khz sampling rate should be fine, right?

First, to start off simple, let's assume that the NyQuest theorum is correct at face value, and that the highest frequency any human can hear is 20khz.  Then a 40khz sampling rate should be 100% perfect.

The first issue we face is something called quantization noise that comes from digitizing the analog signal.  This is basically the error introdoced by rounding.  We call this error "noise" in the case of analog to digital converters simply because it sounds mostly like random noise.  (Note that increasing the bit depth can theoretically decrease noise, but it will never reach zero, since an ADC converts an infinitely variable signal into one with only certain values.  This is the advantage - and disadvantage - of digital).  Aliasing (Audio Moiré patterns) is also an issue.  

To put it simply, the 44.1Khz of standard CDs should be able to store sounds up to 22khz, or some of that space can be devited to create some buffer space to help  lower the qualitization noise (which can be shifted into that frequency range) and Moiré patterns.  

"Monty" of OGG fame even did some neat videos where he not only explains the NyQuest theory, but even demonstrates with some equipment that nearly perfect output can be obtained with only CD quality sampling.  

Yet his videos and other material I have seen and read dance around one thing, the Nyquest theorum really only talks about sine waves.  Monty phrases it using some language like "higher frequency components".  Anything except a sine wave is called a "Complex" wave that will have different components.  

Think about it, if you are sampling at 40khz, and trying to catch a signal at 20khz, you can't actually get that much data, just two points per cycle.  What Nyquest was saying was that assuming you sample evenly, and you sample at twice the frequency of the waves you are trying to sample, then you will always have two points per cycle that will give you enough information to fill in the rest, assuming it's a sine wave.  

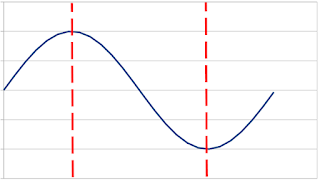
So see what I mean, consider the graph below.  We take two samples during the wave form.  If we know that it's a sine wave we are sampling, then the two points we took here give us enough information to know both the aplitude (loudness) and freqeuency (pitch).  From just that data we can reconstruct the entire curve.  

And that's absolutely true, and it's also a really great observation.  But what happens when we're not talking about sine waves?

How about a square wave?

A sawtooth wave?

Note: I am purposely using slightly imperfect waves here, like you might see in the real world.  

The point is that you could have the same two sample points of +1 and -1, and if you aren't restricted to sine waves, then you could create an infinite number of possible wave forms!

So the next question is - does this even matter for music?

Sure it does!  Musical instruments don't generate simple pure tones.  String instruments such as chellos, violins, etc. create sawtooth waves because of the way their strings stick to the bow and then release suddenly.  

Clarinets and Saxophones also produce modified square waves.   

There are also triangle waves and many other types.  For example, a wave form from a harmonica does not look the same as one from a harpsicord.  

There are many other types of waves produced by other instruments.  Even if you don't know the technical details, you know that a piano and a saxophone sound different even when they play the same note (such as a middle C) - and part of that is due to the wave form.  Admittedly, other reasons include different overtones, etc.  

And I believe that it is indisputable that just given two points in a single cycle, there is no way to know what type of wave the source material is.  

Now, it is true that we are typically not trying to reproduce piano, clarinet, or violin sounds at 20Khz often - but consider that what I showed above was just the most extreme case.  

Looking at the graphs above, how many points would you want to have for one cycle of the wave?  (Yes, I cheated a bit on the sawtooth example, but a triangle wave would have been spot on).

In fact, even doubling our sampling frequency from 40khz to 80khz doesn't guarantee us the best results in all cases!  

In our somewhat contrived example where we start at the top of the cycle, we would get 4 samples per cycle, but they would be at +1. 0, -1, and 0 for both the sine wave and realistic imperfect square wave.   I'll even add in a triangle wave as a bonus.  

This means in this case, sampling at 80Khz still wouldn't give us enough information to reproduce this wave accurately.  

Still, this is close to ultrasonic, so even if you can hear it, you probably can't tell what kind of wave it is, right?  Honestly, I have no idea.  I can hear sounds at 20Khz with no issues, but they are mainly very annoying, not something I try to savor, analyze, and enjor.  

Further Thought Experiments

But what about something like the range between 1Khz and 3.5Khz, which is usually considered to be the most dsensitive range for humans (The "mids")?

  

Well the good news is that at 44Khz, a 1 khz wave will be sampled 44 times per cycle!  That's enough to generate a pretty good wave form!  

A 2 Khz signal will only get 22 samples per cycle allocated, but 22 samples is still not too bad.  (If you don't believe that, note that I only used 26 samples to create the sine wave in the graph above, and it still looks smooth to me).

At 3.5Khz, we're down to 12 samples, which is still a lot better than 2 or 4.

Going up to 8khz, we are down to 5.5 samples.  To put things in perspective, the highest note on a normal piano, the C8 is around 4.1Khz, which would still give us ~10.5 samples.

So, as you can see, the number of samples per cycle must necessarily go down as the frequency goes up.  Therefore we slide gradually from having very complete coverage of the wave work to just being able to detect that there is a cycle at all as we go up the scale to 20Khz.  This is convenient, since our hearing gets less detailed as we go up the scale as well.  

One thing to point out is that for normal frequencies, different wave forms do sound very different to most people.  If you don't believe me, listen for youself here.  

It is simply not possible for only sample 2 points per cycle to determine what shape the original wave forms were, and therefore we are certainly losing information about the signal.  Whether that information matters or not is a bit of a different issue.

I would suggest that we don't necessarily need higher frequency in able to record ultrasonic sounds that we can't hear.  For example, I am very annoyed by ultrasonic sounds all the time, but even I can't hear 30Khz, so there is no need to get an 60Khz sampling rate to record and preserve 30khz audio for anyone. (Anyone human at least)

On the other hand, using a 60Khz or 80Khz rate instead of 44Khz  would mean that the middle C discussed above would get ~14.5 or ~19.5 samples devoted to it instead of just ~10.7.  Whether this different actually matters, and under what situations, can only be determined by double blind testing.  

Some reasons why it will matter less than you think:

1. Some instruments do emit sounds with waveformss close to sine waves (e.g. the higher notes on pianos)

2. Even if the sampling system and DAC did not convert the output to sine waves, other factors conspire to do this.  For example, if you pass a square wave through a transformer, it will get a bit closer to a sine wave.  

This means that even if you use a 500Khz sampling frequency, the sound of a Piano wouldn't change much, and though you might get a super accurate shape for the sawtooth waveform of some string instruments, your amplifier and speakers might conspire to dull that sound somewhat back towards being something closer to a sine wave anyway.  

Bottom line:

The answer is not as simple as either camp makes it out to be.  

A pure sine wave can be recomposed with a sampling frequency only twice the frequency we want to reproduce, and 20Khz is fine for music, meaning that a 44Khz sampling rate gets the job done.

The "It's what the pros use, so it must be better" argument is not really sensible when you consider that they have to use higher quality recordings for mixing than you need for listening.  Higher sampling rates give more room for noise shaping, etc.  

On the other hand, we may be inadvertantly blunting our sounds by converting them to sine waves more and more the higher we go up the frequency scale.  

I know this is the kind of thing people are passionate about, so go ahead and tell me why I'm wrong :)